何謂二元搜尋樹（Binary Search Tree）

二元搜尋樹（Binary Search Tree, BST）是一顆 Binary Tree。可為空樹，若非空則：

1. root 左子樹上的所有 node 值，皆小於 root 的 node 值。
2. root 右子樹上的所有 node 值，皆大於 root 的 node 值。
3. root 左右子樹皆為二元搜尋樹。

這就是一個二元搜尋樹。

如何利用二元搜尋樹進行排序？

先將資料建成 BST 後：
根據 BST 的定義，左子樹的值都比樹根小，右子樹的值都比樹根大。
所以用**中序（inorder traversal）**追蹤即可，因為其為 L D R，剛好為小到大。
以上面的圖為例：
中序追蹤為：1 3 4 10 11 12 15 即為小到大排序。

如果要大到小呢？

那就使用 Stack 將 小到大反序就好！

二元樹的新增節點（Insert）

先來定義 Node 的結構：

typedef struct treenode{
    int data;
    struct treenode* lchild;
    struct treenode* rchild;
}treenode_t;

畢竟二元搜尋樹也是一棵二元樹，因此他的演算法跟遞迴脫不了關係的。

觀念：

（假設資料不會重複）
先跟 root 比較，若比 root 小，則到左子樹新增該節點，若比 root 大，則到右子樹新增該節點。直到 root 為空，才在該位置新增節點。

演算法：

treenode_t* BinarySearchTree::insert(treenode_t* root, int x){
    if(root == null){
        treenode_t* newNode = new treenode_t;
        newNode->data = x;
        newNode->lchild = nullptr;
        newNode->rchild = nullptr;
        return newNode;
    }else{
        if(x > root->data){
            root->rchild = insert(root->rchild, x);
        }else{
            root->lchild = insert(root->lchild, x);
        }
    }
    return root;
}

圖示：

二元樹的刪除節點（delete）

觀念：

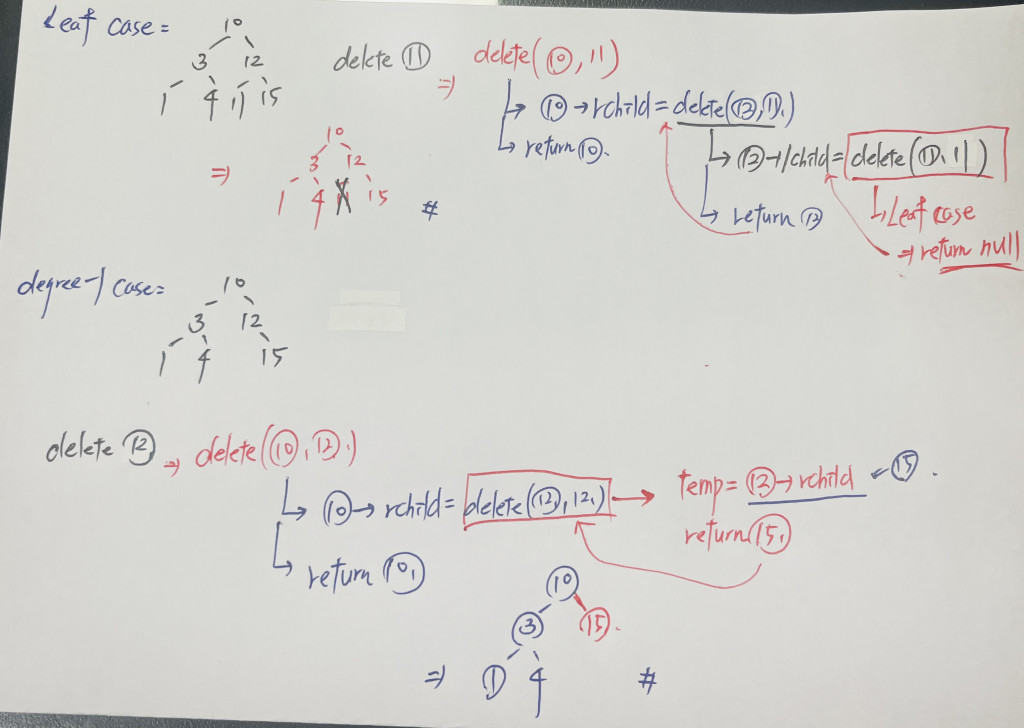
先 search 到該資料後，分成三個 case 處理

1. 樹葉：如果要刪除的節點是樹葉節點，則直接刪除。
2. degree-1 節點：如果這個節點分支度為一，則將原本其父點的連結，連至該子樹
3. degree-2 節點：這個最重要，當左右子樹皆存在時，先選擇左子樹之最大值，或右子樹之最小值，設該點為 Y 點，用 Y 取代要刪除的節點，並改成刪除 Y 點。因為 Y 必為 degree-1 或 leaf，因此回到上面case。
   因為 Y 是左子樹最大值，代表他的 rchild 必為 null（沒東西比他大了）。Y 若是右子樹最小值，代表他的 lchild 必為 null（沒東西比他小了）

演算法：

treenode_t* BinarySearchTree::delete(treenode_t* root, x){
    if(x < root->data){
        root->lchild = delete(root->lchild, x);
    }else if(x > root->data){
        root->rchild = delete(root->rchild, x);
    }else{
        // node found
        if(root->lchild == nullptr && root->rchild == nullptr){
            // leaf case
            delete root;
            return nullptr;
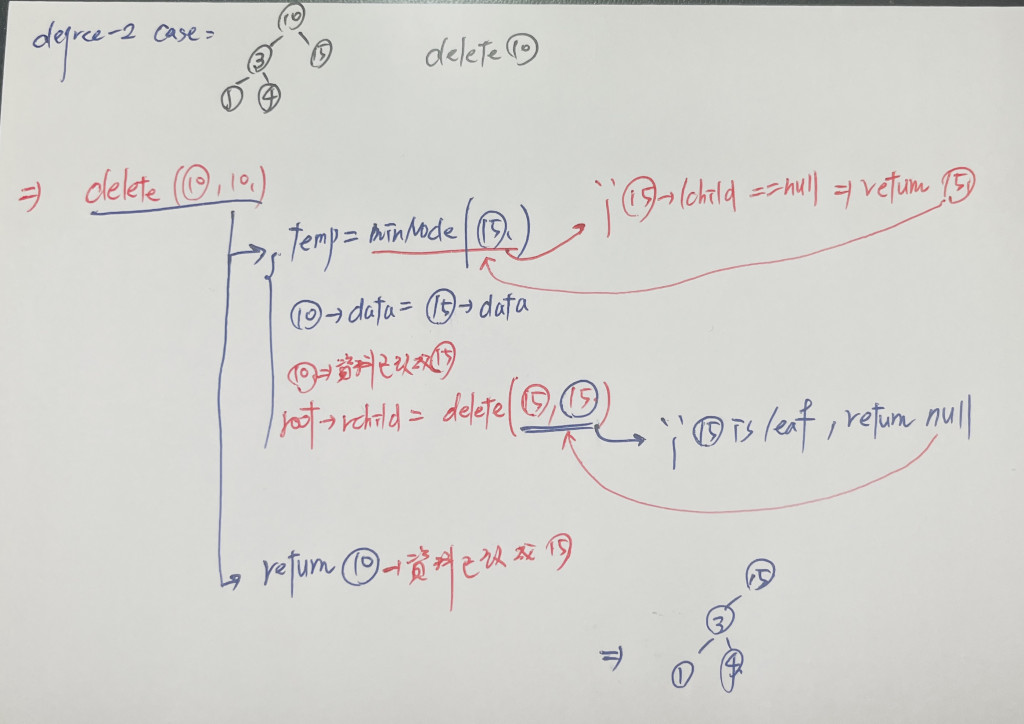
        }else if(root->lchild != nullptr && root->rchild != nullptr){
            // degree-2 case
            treenode_t* temp = minNode(root->rchild);
            root->data = temp->data;
            root->rchild = delete(root->rchild, temp->data);
            /*
            treenode_t* temp = maxNode(root->lchild);
            root->data = temp->data;
            root->lchild = delete(root->lchild, temp->data);
            */
            return root;
        }else{
            //degree-1 case
            if(root->rchild != nullptr){
                treenode_t* temp = root->rchild;
                delete root;
                return temp;
            }else{
                treenode_t* temp = root->lchild;
                delete root;
                return temp;
            }
        }
    }
}

treenode_t* BinarySearchTree::minNode(treenode_t* root){
    if(root->lchild != nullptr){
        return minNode(root->lchild);
    }else{
        return root;
    }
}

treenode_t* BinarySearchTree::maxNode(treenode_t* root){
    if(root->rchild != nullptr){
        return minNode(root->rchild);
    }else{
        return root;
    }
}

圖示：

Binary Search Tree 的問題

Binary Search Tree 的 新增 刪除 查詢的動作，皆跟樹高有關：O(H)，但其可能斜曲，導致時間變成 O(n)，為了解決這個問題，明天要來介紹，高度平衡的二元搜尋樹：AVL Tree。